Dans la première partie, nous avons remis en question la façon habituelle d'évaluer l'erreur absolue moyenne en prenant simplement la différence entre la moyenne prédite et le résultat observé. Nous avons constaté qu'il est nécessaire d'utiliser le bon estimateur ponctuel, la médiane, pour résumer la distribution par un seul chiffre, conformément à l'interprétation opérationnelle de l'erreur absolue. Cela implique toutefois un certain nombre de propriétés désagréables de l'EAM : elle est grossière, discontinue et inutile pour les personnes qui se déplacent lentement.
Préparer le terrain pour la note de probabilité classée
Il est clair que la situation que je vous ai laissée dans la première partie de ce billet n'est pas satisfaisante : L'EAM est discontinue, imprécise, et même inutile pour les élèves à faible progression dont les moyennes prédites sont inférieures à 0,69. Néanmoins, son interprétation commerciale raisonnable - le coût est proportionnel à l'erreur - reste attrayante. Pouvons-nous y remédier ?
Pourrions-nous simplement abandonner la médiane et utiliser un autre résumé, comme la moyenne, beaucoup plus bienveillante ? Malheureusement, prétendre que la distinction médiane/moyenne n'est pas pertinente n'y change rien. Cette voie ne résout pas nos problèmes, mais en introduit de nouveaux : La prédiction qui l'emporterait avec un MAE mal évalué serait biaisée.
Quelles sont alors nos possibilités d'améliorer l'EA, étant donné que nous sommes liés à la médiane en tant que résumé ? Il y a un aspect que nous pouvons modifier, à savoir l'ordre des deux processus "résumer" et "calculer l'erreur". Actuellement, nous commençons par résumer (distribution mise en correspondance avec l'estimateur ponctuel), puis nous calculons l'erreur ("estimateur ponctuel - résultat"). Prenons une grande respiration et échangeons les deux étapes, comme illustré dans le graphique ci-dessous (partie gauche) : Étant donné une distribution prédite (rouge) et un résultat observé (bleu), calculons l'AE pour chaque résultat prédit (flèches noires) :
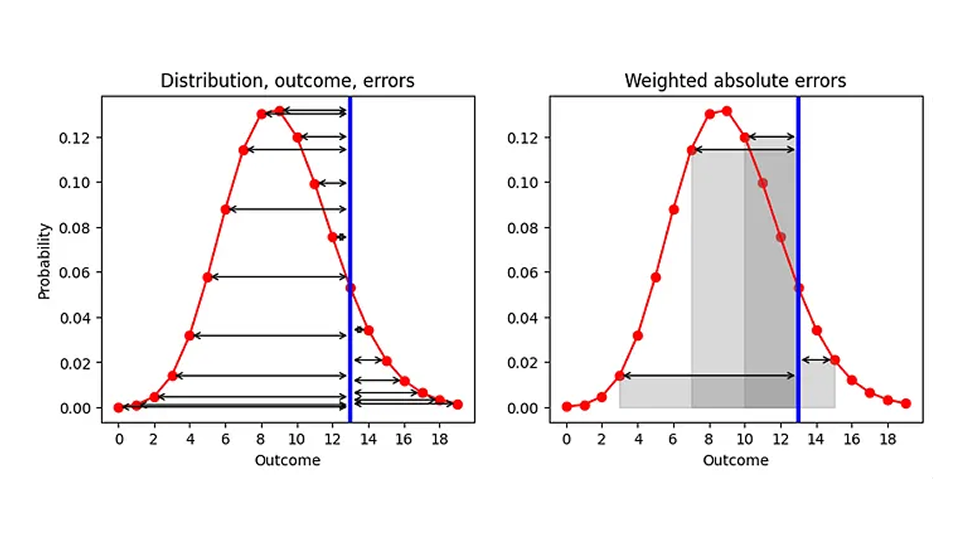
Le résultat est une liste d'AE, un pour chaque résultat (y compris pour la prédiction qui correspond au résultat réel, pour laquelle AE est 0). Puisque notre objectif est de remplacer AE par un seul numéro, nous devons résumer ces nombreux AE. Prenons la moyenne des EA, avec la probabilité que nous avons attribuée à chaque résultat comme poids dans cette moyenne. Géométriquement, nous additionnons les zones délimitées par les flèches d'erreur et l'axe des x, comme illustré pour quelques résultats dans le graphique de droite.
Cette prescription est une définition raisonnable de la distance entre un nombre et une distribution de probabilités : Vous pondérez chaque distance par rapport à un résultat possible par la probabilité attribuée à ce résultat. À titre d'exemple, si la distribution est égale à 0 partout sauf pour un résultat, pour lequel elle est égale à 1 (une prévision déterministe qui prédit que ce résultat se réalisera certainement), nous retrouvons l'AE traditionnel : la valeur absolue de la distance entre ce résultat prédit de manière déterministe et l'observation. Notre AE amélioré devient l'AE traditionnel pour les prévisions déterministes !
Nous pouvons exprimer la prescription par la formule suivante :
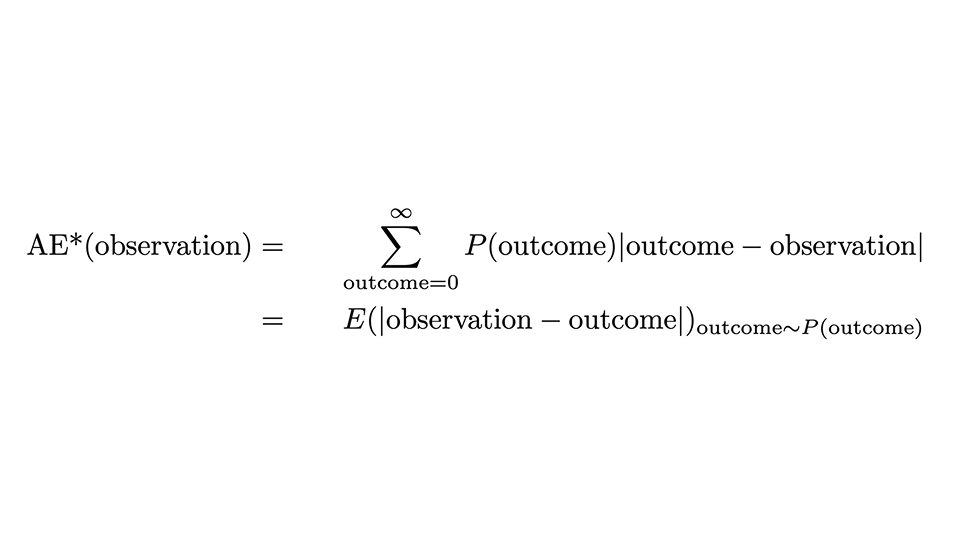
Cela a l'air un peu effrayant, mais passons doucement en revue : L'AE*, l'"AE corrigé", pour une observation est l'AE pour cette seule observation, mais moyenné sur tous les résultats possibles (la somme sur les résultats), avec la probabilité prédite P(résultat) comme poids. La deuxième ligne indique que cela coïncide avec la valeur attendue de la distance absolue entre l'observation et le résultat, lorsque le résultat est distribué selon la loi de probabilité.
Quelle balade ! Nous n'en sommes pas encore là, mais presque : l'AE* n'est pas exactement la note de probabilité classée, et nous n'avons toujours pas la moindre idée de l'origine de ce nom encombrant.
L'AE* défini ci-dessus présente une propriété indésirable : Lorsque la vraie distribution est une distribution de Poisson avec une certaine valeur moyenne, l'AE* le plus bas et le meilleur n'est pas obtenu en faisant correspondre cette valeur moyenne, mais pour une valeur légèrement plus petite. Si votre prévision gagne à AE*, elle est probablement biaisée et sous-estimée. La raison en est que la largeur absolue de la distribution augmente avec la valeur moyenne, ce qui favorise les petites valeurs moyennes (une fois de plus, c'est l'occasion de faire de la publicité pour les articles précédents du blog [liens vers Forecasting Few is Different 1&2]). Ce problème peut être résolu : Nous devons soustraire la moitié de la largeur attendue de la distribution pour en tenir compte, c'est-à-dire la distance attendue entre deux résultats aléatoires tirés de la distribution prédite. Enfin, nous obtenons la note de probabilité classée:
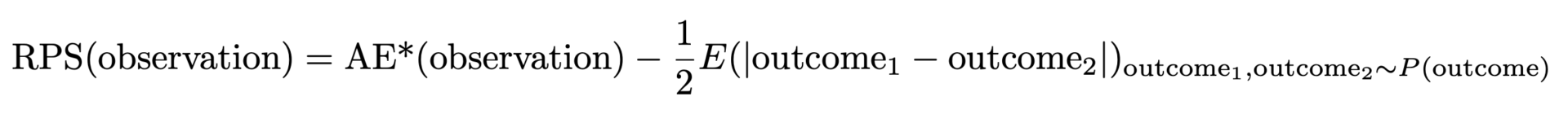
Mais pourquoi ce système s'appelle-t-il Ranked Probability Score (RPS) et pourquoi est-il si impopulaire ? Le SRP est généralement introduit par des formules abstraites contenant de nombreuses probabilités, des fonctions d'étapes, des probabilités cumulatives. Elle est souvent présentée avec une interprétation purement fondée sur la théorie des probabilités, qui a beaucoup de sens si vous vous intéressez à la théorie des probabilités et aux statistiques, mais qui reste inaccessible aux praticiens. Il est vraiment remarquable que les deux formulations - notre "AE améliorée" et celle de la théorie des probabilités - coïncident : Le vilain petit canard (aux yeux du praticien) devient un magnifique cygne.
Comment le score de probabilité classée résout les problèmes de l'erreur absolue moyenne
Dans la première partie de ce billet, j'ai expliqué que l'EAM possède des propriétés peu pratiques : Elle est grossière, discontinue et inutile pour les personnes qui se déplacent lentement. Le RPS, le "MAE amélioré", résout-il ces problèmes ? En effet, c'est le cas !
Dans le graphique suivant, le RPS (ligne noire) est comparé à l'AE (ligne bleue), toujours pour une observation de 9 (ligne pointillée rouge). Pour les prévisions éloignées du résultat 9, le RPS et l'AE se comportent de manière similaire, et le RPS reste légèrement inférieur à l'AE. Lorsque la moyenne prédite et l'observation coïncident à 9, AE atteint zéro, tandis que RPS est un peu plus sceptique : Comme RPS connaît la distribution, il estime que le fait que le résultat corresponde exactement à la médiane de la distribution prédite pourrait également être dû au hasard : Peut-être que le véritable taux de vente ce jour-là était de 7, et que nous avons eu un peu de chance que la demande observée soit de 9. Par conséquent, RPS ne touche jamais 0 : aucun résultat individuel ne prouve sans ambiguïté qu'une prédiction probabiliste était correcte. Lorsque l'on s'éloigne du résultat 9, l'EA est stricte et pénalise immédiatement le fait d'être en décalage avec le coût correspondant. Le SRP est plus bienveillant et n'augmente pas aussi rapidement que l'AE, ce qui montre que le fait d'être un peu à côté de la plaque peut être dû à la malchance et qu'il n'est pas nécessaire de le sanctionner immédiatement. Cela correspond beaucoup mieux à la réalité de l'entreprise : Les opérations sont souvent planifiées de telle sorte que de légers écarts sont tolérables. Tout le monde souhaite, mais personne ne s'attend sérieusement à une prévision déterministe, et il existe des stocks de sécurité pour en tenir compte. Lorsque les écarts sont plus importants, ils commencent à induire des coûts réels.
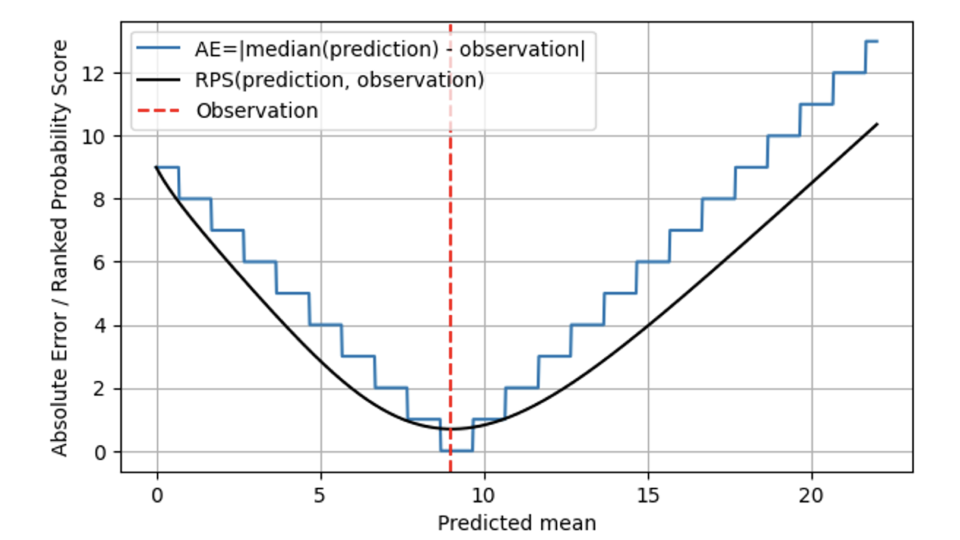
Globalement, la note de probabilité classée ne "saute" pas entre différentes valeurs, mais elle est, mathématiquement parlant, continue dans la moyenne prédite. Pour AE, les prévisions de 8,7, 9,3 et 9,6 sont indiscernables ; pour RPS, elles le deviennent : Le SRP minimum est atteint exactement à une moyenne prédite de 9.
Pour les produits à rotation lente, le SRP est utile, mais ce n'est pas une pilule magique : Il restera toujours difficile de distinguer un produit qui se vend une fois tous les 100 jours d'un produit qui se vend une fois tous les 200 jours, même si vous utilisez le SRP. Néanmoins, le RPS prend des valeurs différentes même pour des prédictions différentes de petite taille comme 0,6, 0,06 et 0,006.
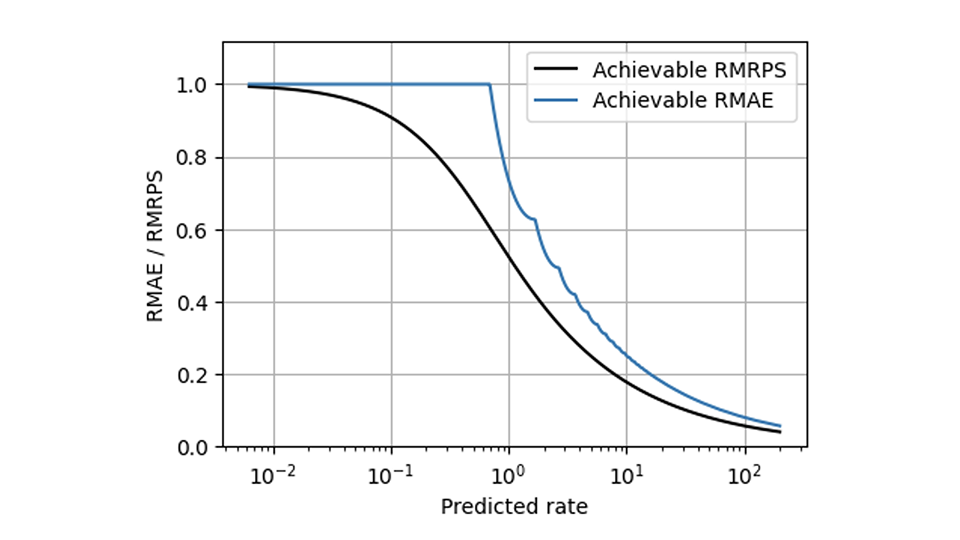
Le RPS permet de résoudre de nombreux problèmes de MAE, mais il en est un que même le RPS ne résout pas : L'inévitable mise à l'échelle qui fait que les vendeurs lents et les vendeurs rapides se comportent différemment. Les méthodes qui rendent les mesures sensibles à l'échelle (décrites en partie dans ce blog [liens vers Forecasting Few is different 1&2]) peuvent toutefois être appliquées aux SRP de la même manière qu'elles l'ont été à l'AE. Comparé au MAE relatif, le RPS moyen relatif (le RPS moyen divisé par l'observation moyenne) a une forme beaucoup plus lisse dans ce graphique, ce qui montre la meilleure valeur réalisable pour les deux mesures :
Quand devriez-vous utiliser MRPS au lieu de MAE ?
Les prévisions significatives ne sont jamais déterministes et certaines, mais probabilistes et incertaines, ce qui doit être pris en compte dans l'évaluation. Dire que les humains n'aiment pas l'incertitude est un euphémisme : Les humains détestent l'incertitude. Les gens sont prêts à compromettre une grande partie de l'utilité attendue pour obtenir une certitude parfaite (ce qui est, lorsque le risque est fatal, une chose raisonnable à faire). Lorsqu'on dit aux parties prenantes qu'une prévision ne fournit "que" des prévisions probabilistes, elles veulent souvent une prévision déterministe, et les prévisionnistes doivent les décevoir en refusant d'établir une telle prévision. Mais rendre explicite l'incertitude inévitable n'est pas un signe de faiblesse, mais de confiance.
Condenser en un seul nombre tout le pouvoir d'expression d'une distribution de probabilités, qui contient la probabilité de chaque résultat imaginable, est aussi simpliste, grossier et brutal qu'il y paraît - même si c'est ce que vous devez faire de manière opérationnelle lorsque vous faites des réserves. D'un point de vue conceptuel, la note de probabilité classée donne donc une bien meilleure réponse à la question "quelle est la distance entre le résultat et la prédiction" que l'erreur absolue.
Lorsque la nature probabiliste de la prévision n'est pas pertinente, la différence entre l'EA et le SRP devient négligeable, et l'EA et le SRP peuvent être utilisés de manière interchangeable (le premier étant plus simple à calculer que le second, le second supposant des valeurs légèrement inférieures). En d'autres termes, lorsque la largeur de la distribution de probabilité est beaucoup plus petite que les erreurs typiques qui se produisent, je ne pourrai pas, en tant que prévisionniste, imputer les erreurs qui se produisent à un "bruit inévitable contre lequel on ne peut rien faire". Par exemple, lorsque je prévois que certains articles se vendront 1000 fois, alors que je ne suis pas particulièrement ambitieux et que je serais déjà satisfait si les résultats se situaient entre 800 et 1200, la différence entre l'utilisation du RPS et de l'AE devient marginale. Par souci de simplicité, je devrais donc m'en tenir à l'AE.
Lorsque nous touchons au régime à évolution moyenne ou lente, c'est-à-dire lorsque nous prévoyons des valeurs moyennes telles que 0,8, 7,2 ou 16,8, il est important de savoir si nous condensons la distribution en un seul chiffre pour évaluer l'AE ou si nous suivons la voie un peu plus complexe de l'ERS. Lorsque nous prédisons "1", nous voulons dire que la probabilité d'observer "1" est d'environ 37%, tout comme la probabilité d'observer 0. Il est donc dangereux et trompeur de négliger la nature probabiliste des prévisions dans le régime des ventes moyennes à lentes. Mais vous savez maintenant comment tenir compte de la distribution des probabilités : En utilisant la note de probabilité classée, qui, je l'espère, vous apparaît maintenant comme le beau cygne de la faune de l'évaluation des prévisions, qui réussit à rendre heureux à la fois les statisticiens et les praticiens.













