L'erreur absolue moyenne est le premier choix des praticiens lorsqu'il s'agit d'évaluer leur modèle, en raison de sa définition simple et de sa pertinence commerciale intuitive. La mesure d'évaluation Ranked Probability Score, en revanche, n'est pas vraiment une fonction charmante à première vue : son nom dissuasif correspond bien à sa définition formelle lourde, ce qui explique que presque aucun praticien de la chaîne d'approvisionnement ne la connaisse, et encore moins ne l'utilise. Mais ils passent à côté ! La note de probabilité classée est l'extension naturelle de l'erreur absolue moyenne au domaine des prévisions probabilistes, c'est-à-dire aux prévisions qui "connaissent" leur propre incertitude. Il s'accompagne d'une interprétation intuitive et résout plusieurs problèmes importants liés à l'erreur absolue moyenne. La note de probabilité classée reflète encore mieux l'activité que l'erreur absolue moyenne, et elle tient compte de l'incertitude statistique, réconciliant ainsi la théorie statistique de la tour d'ivoire avec la pratique quotidienne.
Une norme commerciale plausible : Erreur absolue moyenne
"Quelle mesure devons-nous utiliser pour évaluer le modèle de prévision de la demande ?
La réponse à cette question est généralement donnée par l '"erreur absolue moyenne", sur des bases tout à fait solides. L'erreur absolue (AE) reflète souvent de manière raisonnable le coût d'une prévision "erronée". Lorsque je prévois la vente de 8 paniers de fraises, que je stocke 8 paniers, mais que la demande réelle est de 9, j'ai une EA de 1, et 1 client mécontent se tourne vers la concurrence. Lorsque ma prévision est de 11 paniers pour la même demande de 9, l'AE est de 2, et j'ai 2 paniers de fraises à écouler. Pour ce résultat observé 9, l'AE est représenté par la ligne bleue dans le graphique suivant en fonction de la prédiction :
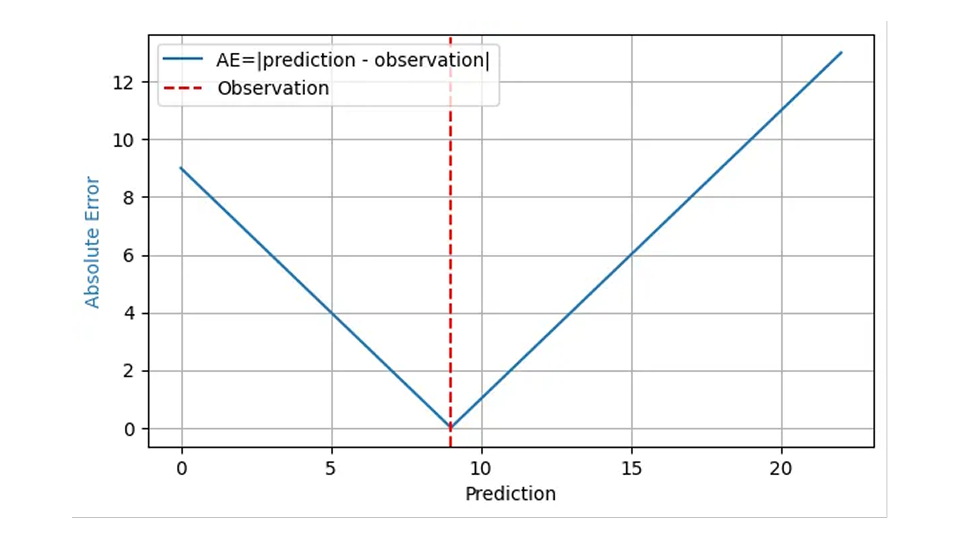
Étant donné que l'impact financier d'une erreur de prévision est généralement proportionnel à l'erreur de prévision elle-même, la moyenne de l'AE pour de nombreuses prévisions et résultats, l'erreur absolue moyenne (EAM), reflète le coût de l'entreprise, du moins si l'on part du principe qu'une pièce de surstock a le même impact financier qu'une pièce de sous-stock. L'erreur quadratique moyenne (EQM) indiquerait qu'il est d'autant plus coûteux de se tromper d'une unité que l'erreur est importante, ce qui est tout à fait irréaliste dans le monde des affaires. L'erreur absolue moyenne en pourcentage (MAPE), la moyenne de l'EA normalisée, Moyenne (EA/résultat observé), souffre de sérieux écueils inattendus(comme décrit dans ce précédent billet de blog), et peut être rejetée en toute sécurité pour la prévision de la demande.
Par conséquent, il est conseillé aux praticiens d'utiliser l'EAM ou sa variante normalisée, l'EAM relative (EAMR) = EAM / Moyenne (résultat), comme premier choix simple pour évaluer leurs modèles. Les valeurs typiques de MAE et de RMAE dépendent toutefois de l'échelle : Les prévisions concernant les bouteilles de lait (ventes rapides) seront naturellement accompagnées d'un MAE plus important et d'un RMAE plus faible que les prévisions concernant certaines piles spéciales (ventes lentes). C'est pourquoi la contribution du blog consacrée à cette question n'a même pas fait l'objet d'un seul article, mais a été divisée en deux parties :Forecasting few is different (1) et Forecasting few is different ( 2).
MAE étant simple, bien connu et pertinent, pourquoi écrire ou lire un article de blog sur une alternative ? Faire aveuglément confiance à une mesure d'évaluation est certainement l'une des choses les moins scientifiques à faire. Faisons un examen approfondi du MAE pour voir s'il se comporte vraiment comme nous le pensons et, si ce n'est pas le cas, comment y remédier. Pour faire court : vous rencontrerez quelques complications inattendues et désagréables lors de l'évaluation de l'EA, mais elles sont résolues en douceur par une mesure connexe mais très sous-estimée, la note de probabilité classée.
Attendez, pas si vite ! Comment évaluer l'erreur absolue moyenne pour les prévisions probabilistes ?
Jusqu'à présent, nous avons fait comme si "une prévision" était simplement un nombre, tout comme l'objectif prévu lui-même (le nombre d'articles vendus, qui peut être le nombre de paniers de fraises, de pommes, de bouteilles de lait ou de t-shirts rouges). Calculer la différence entre cette prévision (un nombre) et l'observation réelle (un autre nombre) ne pose alors aucun problème : je prévois la vente de 10 pommes, 7 ont été vendues, l'AE est de 3. Aucun doctorat en statistiques n'est nécessaire.
Mais il y a une subtilité : et si j'avais prédit la vente de 10,4 pommes au lieu de 10 ? Quelle aurait été ma décision concernant le stock à conserver ? Il est probable que j'aurais quand même commandé 10 pommes, c'est-à-dire que la petite différence de 0,4 dans les prévisions n'aurait pas fait de différence opérationnelle, le résultat commercial aurait été le même. Néanmoins, l'erreur absolue serait légèrement plus élevée, 3,4 au lieu de 3. L'évolution régulière de l'erreur absolue dans la prédiction de la première figure est trompeuse : La différence entre la prédiction et la réalité n'est pas la quantité pertinente pour l'entreprise, mais plutôt la différence entre le nombre d'articles commandés et la réalité. Pourquoi prévoirais-je alors autre chose qu'un nombre entier, alors que je sais que seules des quantités entières peuvent se produire ?
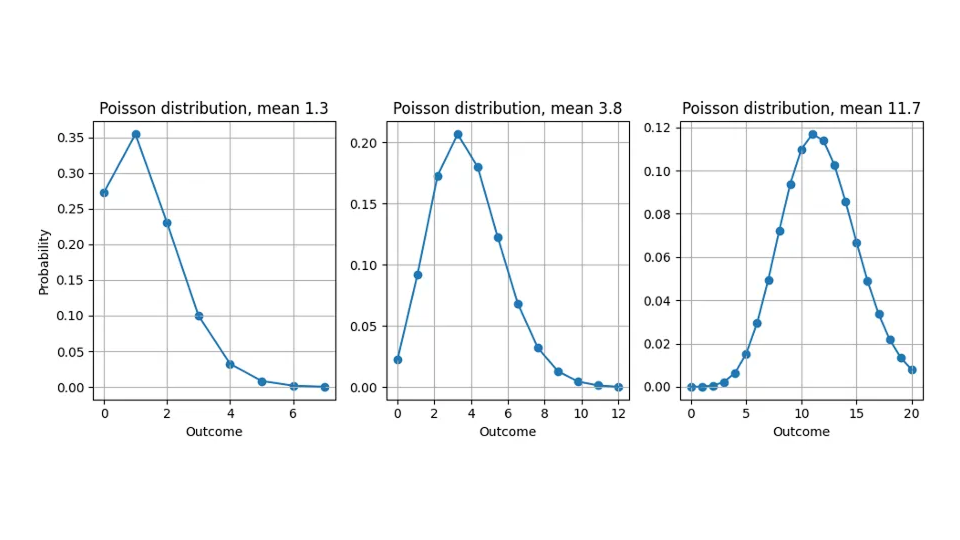
La raison de cette divergence - nous prévoyons des valeurs non entières mais ne mesurons que des quantités entières - est que la plupart des prévisions ne sont pas des "prévisions ponctuelles" qui expriment une "meilleure estimation" universelle, indépendante de l'évaluation, pour la cible, mais fournissent une distribution de probabilités (pas d'inquiétude : aucun doctorat en statistiques n'est encore nécessaire). Ils nous indiquent la probabilité de chaque résultat possible : Lorsque nous prédisons 10,4, nous ne prétendons pas qu'un client coupera une pomme en morceaux pour en acheter 0,4, mais nous estimons que les résultats possibles "11", "12", "13" sont plus probables que pour une prédiction de 10,0. Les prévisions ne sont donc pas de simples chiffres que l'on peut comparer à l'objectif, mais des fonctions. Même si la discussion s'applique à n'importe quelle distribution, je supposerai tout au long de ce billet que la distribution de probabilité prédite est la distribution de Poisson (consultez nos billets de blog à ce sujet ici et ici).
Voyez ici quelle distribution de probabilités nous affirmons implicitement lorsque nous prédisons 1,3, 3,8 ou 11,7 :
Retour à l'évaluation de l'erreur absolue : Comment soustraire une fonction d'un nombre? Soustraire 7 articles vendus d'une distribution de probabilité n'a aucun sens. Nous devons résumer la distribution de probabilité prédite par un seul chiffre pour pouvoir effectuer une comparaison. Ce nombre récapitulatif est appelé l'estimateur ponctuel, qui peut ensuite être soustrait de la valeur réelle observée pour obtenir l'erreur.
Les distributions de probabilités peuvent être résumées de nombreuses façons : La moyenne est la plus immédiate, mais les distributions peuvent également être résumées par leur résultat le plus probable (leur mode), par le résultat qui divise la distribution de probabilités en deux moitiés égales (leur médiane), ou par d'autres prescriptions.
Dans ce zoo d'estimateurs ponctuels, certains semblent plus naturels que d'autres - pouvons-nous simplement choisir le résumé qui nous convient le mieux ? Non, l'estimateur de points correct est fixé par la métrique d'évaluation choisie. En d'autres termes : Vous pouvez choisir la mesure d'erreur qui évalue ma prévision (MAE, MAPE, MSE...), mais je choisis ensuite comment résumer la prévision pour cette évaluation. Mon estimateur de points pour gagner à la MAE sera différent de celui pour gagner à la MSE, sans parler de la MAPE. Ce choix peut vous sembler arbitraire, voire malhonnête, mais il reflète l'immense pouvoir d'expression des prévisions probabilistes : Elles contiennent beaucoup plus d'informations qu'une simple "meilleure estimation". En fonction de la manière dont elles sont évaluées, de la manière dont la "meilleure" est définie par la métrique d'erreur, la valeur qui l'emporte pour une méthode d'évaluation donnée est choisie en conséquence. En d'autres termes : La question "Donnez-moi votre meilleure prévision" n'a pas de sens tant que la définition de "meilleure" n'est pas claire. Une prévision probabiliste unique peut produire de nombreux estimateurs de points différents, ou "meilleures estimations", en fonction de la manière dont la prévision est évaluée.
Pour l'erreur quadratique (SE), l'estimateur ponctuel est la moyenne de la distribution. Pour l'erreur absolue en pourcentage (EAP), l'estimateur ponctuel est une fonction vraiment contre-intuitive avec laquelle je ne vous ennuierai pas, qui conduit à des paradoxes inattendus dans les évaluations MAPE.
L'erreur absolue nécessite la médiane de la distribution, et non la moyenne, et oui, cela a de l'importance.
Pour l'AE (erreur absolue), l'estimateur ponctuel correct s'avère être la médiane. Oui, la médiane, et non la moyenne, et non, nous ne pouvons pas utiliser la moyenne à la place. Permettez-moi d'expliquer pourquoi seule la médiane peut être optimale pour l'AE. Prenons une prévision, c'est-à-dire une distribution, et supposons qu'il s'agit de la distribution de Poisson avec une moyenne de 3,8 et une médiane de 4. Combien d'articles achetez-vous lorsqu'on vous donne cette prévision ? Le résultat est nécessairement un entier, il ne peut pas être 3,8. Pour trouver le bon montant de stock, choisissons l'estimation telle que l'AE que nous trouvons en moyenne en observant les résultats de cette distribution soit le plus petit possible.
Nous recherchons le bon estimateur ponctuel qui condense toute cette distribution en un seul nombre, le meilleur montant de stock d'un point de vue opérationnel. Dans cette figure, j'essaie trois estimations différentes (3, 4, 5) :
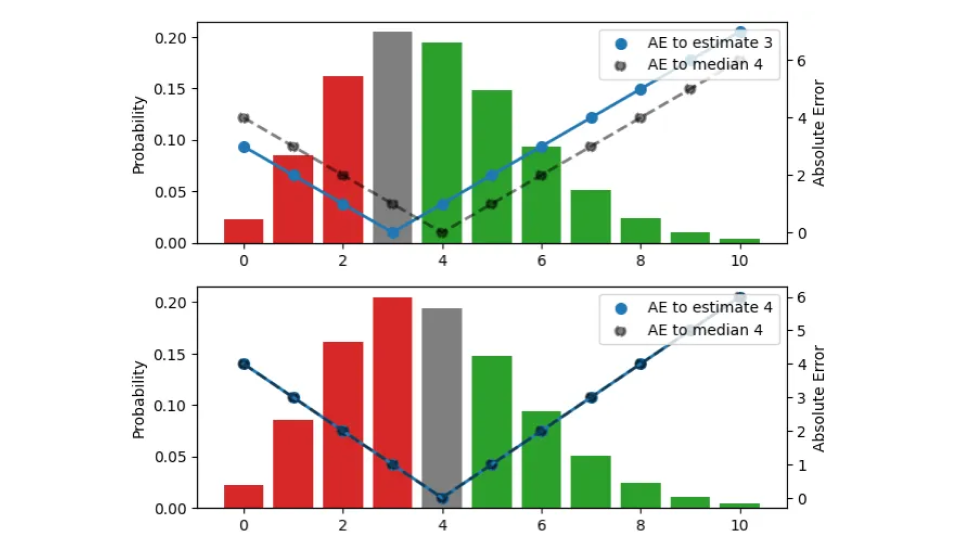

La distribution de probabilité, visualisée par les barres (échelle de gauche), est la même dans les trois panneaux. Le panneau du haut représente l'estimation 3, celui du milieu l'estimation 4 et celui du bas l'estimation 5. L'AE entre l'estimation et les résultats est représentée par les points bleus, reliés par la ligne continue (échelle de droite), l'AE par rapport à la médiane 4 est représentée par les points noirs, reliés par une ligne en pointillés. Par exemple, lorsque l'estimation est 3 (panneau supérieur), l'erreur pour le résultat 3 disparaît et la ligne continue bleue atteint 0. Si l'observation est 4 ou 2, l'erreur est 1.
La couleur des barres indique si un résultat prédit contribue à l'erreur absolue parce qu'il est plus petit (rouge) ou plus grand (vert) que l'estimation, la hauteur de la barre étant la probabilité qu'il se produise. Lorsqu'un résultat correspond à l'estimation, il contribue à zéro à l'erreur et apparaît en gris. En décalant l'estimation d'une unité vers le haut, nous descendons d'un panneau, et toutes les observations sous les barres rouges et sous la barre grise contribuent à une unité d'erreur supplémentaire pour la nouvelle estimation décalée : Pour l'estimation 3 précédente, le résultat 2 avait une erreur de 1, mais pour l'estimation 4, le même résultat a une erreur de 2. D'autre part, toutes les observations qui avaient des barres vertes contribuent maintenant à une unité d'erreur de moins après le décalage : Pour l'estimation 3, le résultat 5 avait une erreur de 2, pour l'estimation 4, l'erreur diminue à 1.
Résumons ce qui se passe lorsque l'estimation est augmentée d'une unité : La valeur attendue de l'AE selon la distribution augmente pour les résultats qui sont inférieurs ou égaux à l'estimation (nous les surestimons encore plus) et diminue pour ceux qui sont supérieurs à l'estimation (nous les sous-estimons moins). L'augmentation est proportionnelle à la surface totale des barres rouges et grises, la diminution est proportionnelle à la surface des barres vertes.
Par analogie, lorsque l'on diminue l'estimation d'une unité, les observations sous les barres vertes ou sous la barre grise contribuent à une unité d'erreur supplémentaire chacune, et toutes les observations dans les barres rouges contribuent à une unité d'erreur en moins.
Pour une distribution donnée, le fait de déplacer l'estimation d'un point vers le haut ou vers le bas augmente ou diminue l'erreur absolue attendue qui en résulte, et nous pouvons rechercher la bonne estimation ponctuelle en cherchant le minimum. Vous avez peut-être déjà élaboré cette règle empirique : si, pour l'estimation actuelle, la plupart des résultats sont inférieurs aux prévisions, diminuez l'estimation ; si la plupart des résultats sont supérieurs aux prévisions, augmentez-la. Ce n'est que lorsque la différence entre les masses de probabilité liées aux sur- et sous-prédictions (la différence entre les surfaces totales des barres "rouges" et "vertes") est inférieure à la barre grise qu'il n'est plus possible d'améliorer l'erreur. C'est le cas dans le panneau du milieu : L'estimation est telle que les masses de probabilité inférieures et supérieures coïncident presque, de sorte qu'un déplacement dans l'une ou l'autre direction augmenterait l'erreur totale. Cette estimation correspond à la médiane : Lorsque vous disposez d'une distribution de probabilités, l'estimateur ponctuel qui minimise l'erreur absolue sera supérieur ou inférieur aux résultats dans la moitié des cas.
Je pense qu'il vaut la peine de souligner ce point, car il n'est souvent pas pris en compte : Lorsque 7,3 est la meilleure estimation de la moyenne d'une distribution, la manière correcte d'évaluer l'erreur absolue par rapport à une observation de, disons, 9, n'est pas de soustraire 7,3 de 9, mais de soustraire la médiane de cette distribution (qui est 7 pour la distribution de Poisson), de 9. Opérationnellement, 7 est précisément le nombre d'articles que vous stockeriez, compte tenu d'une prédiction de 7,3. Étonnamment, il n'est pas utile d'avoir une estimation précise de la valeur moyenne pour les décisions concernant les actions, peu importe que la prévision soit de 7,1 ou de 7,3 : Vous devez vous décider pour un nombre entier. Cependant, lorsque les prévisions sont agrégées à un niveau supérieur pour la planification, la distinction entre 7.1 et 7.3 devient importante.
Cette distinction entre la moyenne et la médiane peut vous sembler couper les cheveux en quatre : Après tout, la valeur qui divise la probabilité en deux moitiés égales et la moyenne de cette distribution semblent très similaires, et elles sont proches pour la plupart des distributions bienveillantes (comme la distribution de Poisson qui est pertinente pour le commerce de détail). Cependant, deux distributions peuvent avoir la même moyenne, mais des médianes différentes ; deux autres distributions peuvent coïncider au niveau de la médiane, mais différer au niveau de la moyenne. L'utilisation de la moyenne et de la médiane comme synonymes vous empêcherait de trouver la meilleure prévision.
Les défauts inattendus de l'erreur absolue moyenne
Nous savons maintenant comment évaluer l'erreur absolue pour les prévisions probabilistes : Nous résumons la distribution par la médiane de l'estimateur ponctuel (le nombre d'articles que nous achèterions), nous soustrayons cette médiane du résultat observé et nous prenons la valeur absolue. J'ai essayé de visualiser cela dans le graphique suivant :
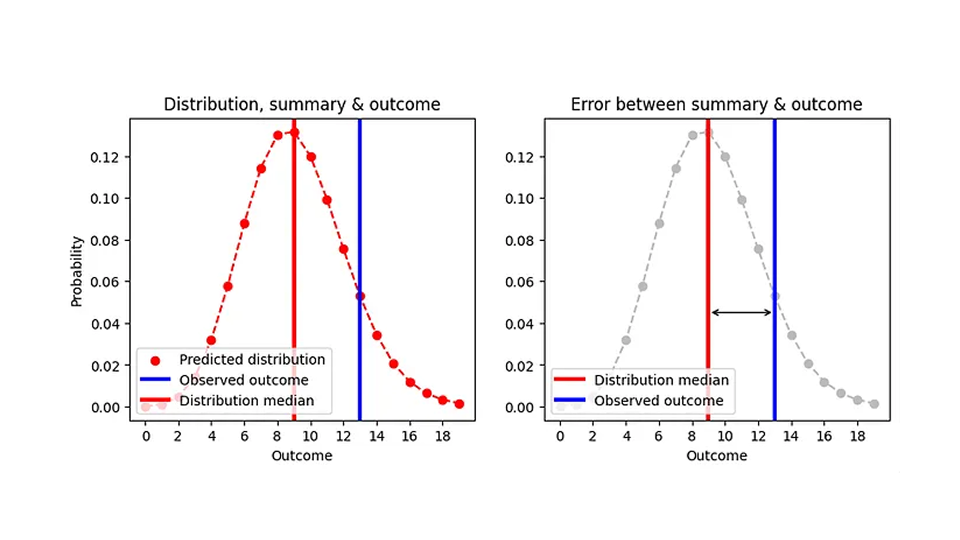
La médiane étant toujours un nombre entier, deux distributions très différentes peuvent donner la même erreur absolue. Par exemple, les AE pour une prévision de Poisson de 8,7 (médiane=9) et pour une prévision de Poisson de 9,6 (médiane=9) sont les mêmes, alors que les prévisions sont clairement différentes, comme le montre cette figure :
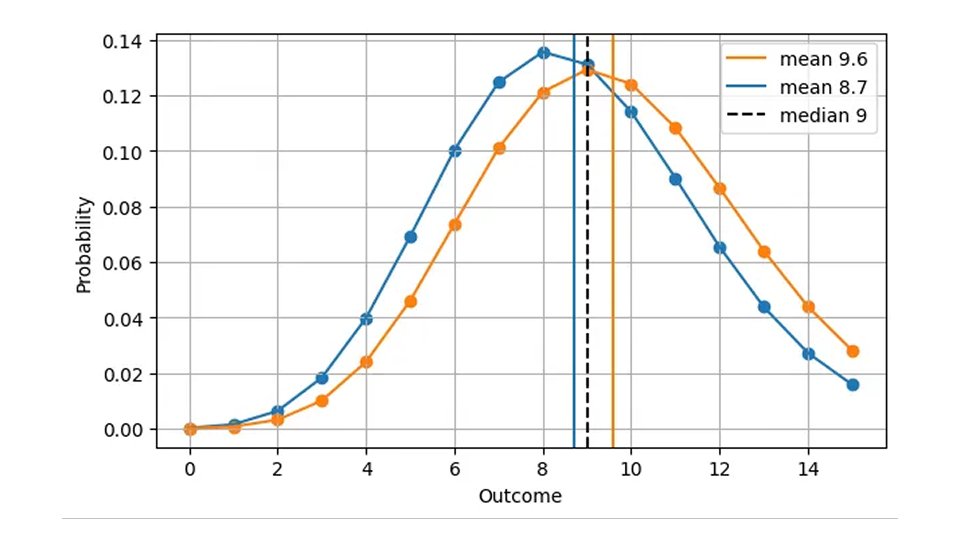
Cela est logique d'un point de vue opérationnel : Dans les deux cas, la bonne chose à faire est d'avoir 9 articles en stock un jour donné. Par conséquent, une version plus réaliste de la toute première figure, AE en fonction de la prédiction, est la suivante.
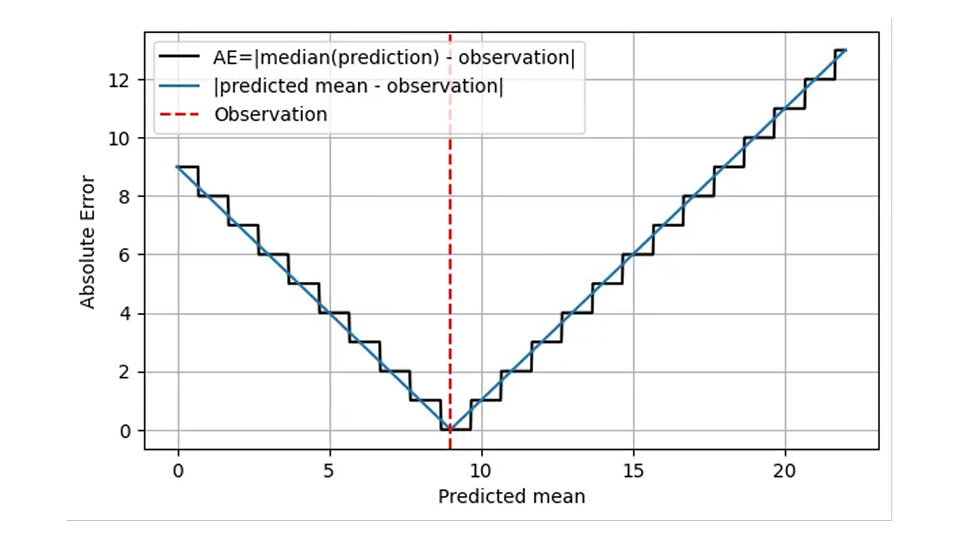
L'AE est calculée en utilisant la médiane de la prédiction (ligne noire) et ne prend que des valeurs entières. Je suis un peu plus précis sur la signification de l'axe des abscisses : Il ne s'agit pas seulement de la "prédiction", mais de la moyenne prédite.
Cette forme d'escalier implique que AE est grossier et imprécis : Nous pouvons, à l'œil, distinguer les distributions de moyenne 8,7 et 9,6, mais AE ne le peut pas ! La MAE seule ne vous aidera pas à améliorer la précision d'une prévision au-delà d'un certain seuil, qui est très élevé pour les objets se déplaçant lentement : La différence relative entre 1,7 et 2,6 s'élève à 53%, alors que l'AE d'une prévision de 1,7 et celle d'une prévision de 2,6 sont identiques ! Ce comportement grossier s'accompagne de sauts désagréables, de discontinuités au niveau des valeurs pour lesquelles la médiane de la distribution passe d'une valeur entière à l'autre. D'un point de vue opérationnel, il n'y a pas de différence entre prévoir 1,7 ou 2,6 pour un jour, un lieu et un article donnés : La bonne quantité à stocker est 2. Les prévisions sont toutefois également utilisées à des niveaux d'agrégation plus élevés pour la planification. À un niveau aussi élevé, on remarque effectivement la différence entre 1,7 et 2,6 : pendant les 100 jours suivants, le fait de commander 170 ou 260 articles au fournisseur fait une énorme différence.
Lorsque la moyenne prédite est inférieure à environ 0,69 par période de prédiction (une vente lente), la prédiction qui vous donne la meilleure erreur absolue est 0. De manière assez spectaculaire, nous avons la même erreur absolue pour une prévision de 0,6, de 0,06 et de 0,006, même si nous sommes passés par deux ordres de grandeur ! La prévision 0 est tout à fait inutile dans la chaîne d'approvisionnement, car vous entrez dans le cercle vicieux des prévisions 0 parfaites : Vous stockez 0, vous vendez 0, et votre prévision précédente de 0 s'est avérée correcte.













