Le biais de sélection a posteriori survient lorsque les prévisions probabilistes et les réalisations observées ne sont pas correctement regroupées lors de l'évaluation de la précision des prévisions en fonction de la fréquence des ventes. D'une part, le biais de sélection a posteriori est un piège insidieux qui vous incite à tirer des conclusions erronées sur le biais d'une prévision probabiliste donnée - dans le pire des cas, il vous fait choisir un modèle moins bon plutôt qu'un meilleur. D'autre part, sa résolution et son explication touchent à des fondements statistiques tels que la représentativité de l'échantillon, les prévisions probabilistes, les probabilités conditionnelles, la régression à la moyenne et la règle de Bayes. En outre, il nous amène à réfléchir à ce que nous attendons intuitivement d'une prévision, et à la raison pour laquelle ce n'est pas toujours raisonnable.
Les prévisions peuvent concerner des catégories distinctes - y aura-t-il un orage demain ? - ou des quantités continues - quelle sera la température maximale demain ? Nous nous concentrons ici sur un cas hybride : Les quantités discrètes, qui peuvent être, par exemple, le nombre de T-shirts vendus un jour donné. Un tel nombre de vente est discret, il peut être 0, 1, 2, 13 ou 56 ; mais certainement pas -8,5 ou 3,4. Nos prévisions sont probabilistes, nous ne prétendons pas savoir exactement combien de T-shirts seront vendus. Une approche réaliste, mais ambitieuse et étroite (c'est-à-dire que l'objectif de l'UE est d'atteindre les objectifs de l'UE). précise) est la distribution de Poisson. Nous supposons donc que notre prévision produit le taux de Poisson que nous pensons être à l'origine du processus de vente réel.
Une prévision plutôt médiocre ?
Supposons que la prévision ait été émise, que les ventes réelles aient été collectées et que la prévision soit évaluée à l'aide de ce tableau :
| Fréquence des ventes observée | Moyenne des ventes observées | Prévision moyenne |
| Lenteur 0, 1, 2, pièces/jour | 0.804 | 1.373 |
| Moyen 3-10 pièces/jour | 5.119 | 4.601 |
| Rapide >10 pièces/jour | 13.880 | 11.041 |
Les données sont regroupées en fonction de la fréquence de vente observée : Nous classons tous les jours dans des groupes où le T-shirt a été vendu peu de fois (0, 1 ou 2), de façon intermédiaire (3 à 10) ou beaucoup de fois (plus de 10). À première vue, ce tableau indique sans ambiguïté que les ventes lentes sont surestimées et que les ventes rapides sont sous-estimées. Les prévisions sont si manifestement erronées que nous nous empresserions de les corriger, n'est-ce pas ?
En réalité, et de manière peut-être surprenante, tout va bien. Oui, les ventes lentes sont effectivement surestimées et les ventes rapides sous-estimées, mais les prévisions se comportent comme elles le devraient. C'est notre attente - que les colonnes "ventes moyennes observées" et "prédiction moyenne" devraient être identiques - qui est erronée. Il s'agit d'un problème psychologique, d'une attente irréaliste, et non d'une mauvaise prévision ! Une prévision probabiliste n'a jamais promis et ne pourra jamais garantir que, pour chaque groupe de résultats possibles, la prévision moyenne corresponde au résultat moyen.
Voyons pourquoi, comment résoudre cette énigme de manière satisfaisante et comment éviter des biais similaires.
Que demandons-nous réellement ?
Prenons un peu de recul et exprimons en mots ce que le tableau révèle. Les données sont classées en fonction des ventes réellement observées, c'est-à-dire que nous filtrons, ou conditionnons, les prédictions et les observations en fonction du fait que les observations se situent dans une certaine fourchette (ventes lentes, moyennes ou rapides). La première ligne contient tous les jours où le T-shirt a été vendu 0, 1 ou 2 fois, sa colonne centrale nous fournit :

c'est-à-dire la moyenne des observations dans le seau dans lequel nous avons regroupé toutes les observations qui sont 2, 1 ou 0 - certainement un nombre entre 0 et 2, qui se trouve être 0,804. La colonne de droite contient la prédiction moyenne attendue pour le même ensemble d'observations,

c'est-à-dire que pour toutes les observations inférieures ou égales à 2, nous prenons la prédiction correspondante et calculons la moyenne de toutes ces prédictions.
A priori, il n'y a aucune raison pour que la première et la seconde expression prennent la même valeur - mais nous aimerions intuitivement qu'elles le fassent : S'attendre à ce que la prédiction moyenne soit égale à l'observation moyenne ne semble pas trop demander, n'est-ce pas ?
| Fréquence des ventes observée | Moyenne des ventes observées | Prévision moyenne |
| Lenteur 0, 1, 2, pièces/jour | E (observation | observation ≤ 2) | E (prédiction | observation ≤ 2) |
| Moyen 3-10 pièces/jour | E (observation | observation ≤ 3, ≤ 10 ) | E (prédiction | observation ≤ 3, ≤ 10] ) |
| Rapide >10 pièces/jour | E (observation | observation ≥ 11) | E (prédiction | observation ≥ 11]) |
Prévision prospective, rétrospective rétrospective
Conformément à leur étymologie, les prévisions sont tournées vers l'avenir et nous fournissent les probabilités d'observer des résultats futurs,
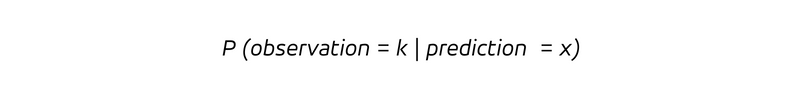
qui est la probabilité conditionnelle d'observer un résultat k, étant donné que le taux prédit est x. Puisque nous avons une probabilité conditionnelle, nous considérons la distribution de probabilité pour les observations en supposant que la prédiction a pris la valeur x. Pour une prévision sans biais, la valeur attendue de l'observation conditionnée par une prédiction x, c'est-à-dire l'observation moyenne dans l'hypothèse d'une prédiction de la valeur x, est :
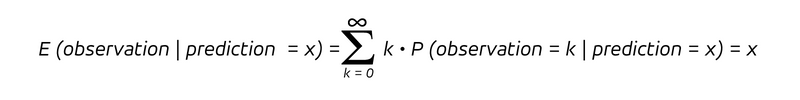
C'est ce que promet toute prévision non biaisée : En regroupant toutes les prédictions de la même valeur x, la moyenne des observations résultantes devrait s'approcher de cette même valeur x. Bien que la distribution puisse prendre de nombreuses formes différentes, cette propriété est essentielle.
Reprenons le tableau : Ce que nous faisons dans la colonne de gauche n'est pas un regroupement/conditionnement par prédiction, mais par résultat. La colonne de droite pose donc la question rétrospective "quelle a été notre prédiction moyenne, compte tenu d'un certain résultat k" au lieu de la question prospective "quel sera le résultat moyen, compte tenu de notre prédiction x".
Pour exprimer la déclaration rétrospective en termes de déclaration prospective, nous appliquons la règle de Bayes,

Les questions rétrospectives et prospectives sont différentes, tout comme leurs réponses : D'autres termes apparaissent, P(prédiction = x) et P(observation = k), les probabilités inconditionnelles d'une prédiction et d'un résultat. Par conséquent, la valeur de l'espérance de la prédiction moyenne, compte tenu d'un certain résultat, devient :

Exemple minimaliste
Quelle est la valeur de E (prédiction | observation = m)? Pourquoi ne pas simplifier à l'observation m ?
Dans la grande majorité des cas, E (prédiction | observation = m) ≠ m est valable. Voyons pourquoi !
Considérons un T-shirt qui se vend de manière égale chaque jour, suivant une distribution de Poisson avec un taux de 5. Le même taux prévu, 5, s'applique à chaque jour. Les résultats sont toutefois variables. Il est clair que 5 est une surestimation pour les résultats 4 et inférieurs, et une sous-estimation pour les résultats 6 et supérieurs. Si nous regroupons à nouveau les résultats, nous rencontrons :
| Fréquence des ventes observée | Moyenne des ventes observées | Prévision moyenne |
| Lenteur <5 pièces/jour | 3.0082 | 5 |
| Moyen 5 pièces/jour | 5 | 5 |
| Rapide >5 pièces/jour | 7.2844 | 5 |
Une fois encore, ce tableau nous permet de conclure que les jours de vente lente ont été surestimés et que les jours de vente rapide ont été sous-estimés, et qu'ils l'ont effectivement été. Elle est valable pour chaque observation E (prédiction | observation = m) = 5, puisque la prédiction est toujours 5.
La prévision est toujours "parfaite" - les résultats se comportent exactement comme prévu, ils suivent la distribution de Poisson avec un taux de 5. L'impression de sous-estimation et de surestimation est purement le résultat de la sélection des données : En sélectionnant les résultats supérieurs à 5, nous conservons les résultats qui sont supérieurs à la prédiction de 5 et qui ont été sous-prédits ; en sélectionnant les résultats inférieurs à 5, nous conservons les événements inférieurs à la prédiction de 5, qui ont été sur-prédits. Pour une prévision probabiliste, il est inévitable que certains résultats aient été sous-estimés et d'autres surestimés. En s'attendant à ce que la prévision ne soit pas biaisée, on s'attend à ce que la sous-estimation et la surestimation s'équilibrent pour une prédiction m donnée. Ce que nous ne pouvons pas espérer, c'est que lorsque nous sélectionnons activement les observations sur- ou sous-prévues, celles-ci ne soient pas sur- ou sous-prévues, respectivement !
Dans une situation réaliste, nous n'aurons pas affaire à une prévision qui suppose la même valeur pour chaque jour, mais la prévision elle-même variera. Néanmoins, sélectionner des résultats "plutôt grands" ou "plutôt petits" revient à conserver les événements sous- ou sur-prévus dans les seaux. Par conséquent, nous avons E (prédiction | observation = m) ≠ m en général. Plus précisément, lorsque m est si grand que le sélectionner revient à sélectionner des événements sous-prévus, nous aurons E (prédiction | observation = m) < m; lorsque m est suffisamment petit pour que le sélectionner revienne à sélectionner des événements sur-prévus, E (prédiction | observation = m) > m.
Prévisions déterministes - vous auriez dû le savoir, toujours !
Pourquoi cela nous laisse-t-il perplexes ? Pourquoi nous sentons-nous mal à l'aise face à cet écart entre l'observation moyenne et la prévision moyenne ? Notre intuition repose sur l'égalité de la prédiction et de l'observation qui caractérise les prévisions déterministes. Dans le langage des probabilités, une prévision déterministe s'exprime : P (observation = prédiction) = 1 et P (observation ≠ prédiction) = 0
Le prévisionniste estime que l'observation correspondra exactement à sa prédiction, c'est-à-dire que les valeurs prédites et observées coïncident avec une probabilité de 1 (ou 100%), tandis que tous les autres résultats sont considérés comme impossibles. C'est une déclaration pleine d'assurance, pour ne pas dire audacieuse. Exprimées sous forme de probabilités conditionnelles, nous pouvons les résumer :

en d'autres termes, chaque fois que nous prévoyons de vendre k pièces (la condition après la barre verticale), nous vendrons k pièces. Puisque le déterminisme n'implique pas seulement qu'à chaque fois que nous prédisons k, nous observons k, mais aussi que chaque observation k a été correctement prédite ex ante comme étant k, nous avons :
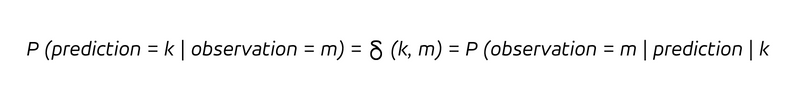
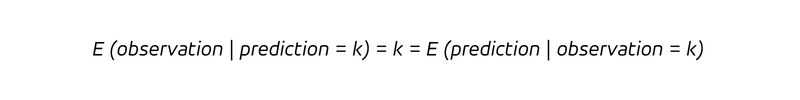
Le déterminisme rend obsolète la distinction entre les questions rétrospectives et prospectives. Avec une prévision déterministe, nous n'apprenons rien de nouveau en observant le résultat (nous le savions déjà !), et nous n'actualisons pas nos convictions (qui étaient déjà correctes).
Dans le cas d'une prévision déterministe de ce type, pour laquelle toutes les distributions de probabilité apparentes s'effondrent pour atteindre un pic de 100% à la seule et unique issue possible, il n'y a pas de biais de sélection a posteriori - nous prétendons avoir su exactement à l'avance, donc nous aurions dû savoir - toujours et dans toutes les circonstances. Si la mesure indique le contraire, votre prévision "déterministe" est erronée.
Toute prévision sérieuse est probabiliste
Les prévisions probabilistes sont plus faibles que les prévisions déterministes, et pour les prévisions probabilistes, nous devons abandonner l'idée que chaque résultat m a été prédit pour être m en moyenne - les prévisions déterministes semblent donc très attrayantes. Mais est-il réaliste de prédire de manière déterministe les ventes quotidiennes de T-shirts ? Supposons que vous ayez pu le faire et que vous ayez prédit que les ventes de T-shirts de demain seront de 5. Cela signifie que vous pouvez citer cinq personnes qui, quoi qu'il arrive (accident, maladie, orage, changement soudain d'avis...), achèteront un T-shirt rouge demain. Comment pouvons-nous espérer atteindre un tel niveau de certitude ? Avez-vous jamais été aussi certain que vous achèteriez un T-shirt rouge le lendemain ? Même si cinq amis promettaient d'acheter un T-shirt demain, quelles que soient les circonstances, comment pourriez-vous exclure que quelqu'un d'autre, parmi tous les autres clients potentiels, achèterait également un T-shirt ? Hormis certains cas très particuliers (très peu de clients, niveau de stock très inférieur à la demande réelle), il est hors de question de prédire de manière déterministe le nombre exact de ventes d'un article. L'incertitude ne peut être maîtrisée que jusqu'à un certain point, et toute prévision réaliste est probabiliste.
Hygiène de l'évaluation
Il existe une autre façon de réfuter le tableau 1 : en établissant le tableau, nous posons une question statistique, à savoir si la prévision est biaisée ou non, et dans quelle direction (ignorons pour l'instant la question de la signification statistique et supposons que chaque signal que nous voyons est statistiquement significatif). Comme toute analyse statistique, une analyse prévisionnelle peut présenter des biais. La façon dont nous avons sélectionné les résultats est un excellent exemple du biais de sélection: Les événements du groupe "vendeurs lents", "vendeurs moyens", "vendeurs rapides" ne sont pas représentatifs de l'ensemble des prédictions et des observations, mais nous les avons regroupés en deux catégories : ceux qui ont été sous-estimés et ceux qui ont été surestimés. Nous avons également utilisé ce que l'on appelle des "informations futures" dans l'évaluation des prévisions : les catégories dans lesquelles nous avons regroupé les prévisions et les observations ne sont pas encore définies au moment de la prévision, mais elles sont établies a posteriori. Par conséquent, le fait d'établir le tableau comme nous l'avons fait viole les principes de base des analyses statistiques.
Régression à la moyenne
Le phénomène que nous venons de rencontrer - les événements extrêmes n'étaient pas prévus pour être aussi extrêmes qu'ils l'ont été - est directement lié à la "régression vers la moyenne", un phénomène statistique pour lequel nous n'avons même pas besoin de prévisions : Supposons que vous observiez une série chronologique de ventes d'un produit qui ne présente aucune saisonnalité ni aucun autre schéma dépendant du temps. Lorsque, un jour donné, les ventes observées sont supérieures aux ventes moyennes, on peut être certain que l'observation du lendemain sera inférieure à celle du jour, et vice versa. Là encore, en choisissant une valeur très grande ou très petite, en raison de la nature probabiliste du processus, nous sommes susceptibles de sélectionner une fluctuation aléatoire positive ou négative, et les ventes finiront par "régresser vers la moyenne". Psychologiquement, nous sommes enclins à attribuer cette régression vers la moyenne - un phénomène purement statistique - à une intervention active.
Résolution : Regrouper par prédiction, et non par résultat. Restez vigilant face aux biais de sélection.
Comment sortir de cette impasse ? En regroupant les résultats, nous sélectionnons des valeurs "plutôt grandes" ou "plutôt petites" par rapport à leur prévision - nous n'obtenons pas un échantillon représentatif, mais un échantillon biaisé. Ce biais de sélection conduit à des groupes qui contiennent des résultats qui sont naturellement "plutôt sous-estimés" ou "plutôt surestimés", respectivement. Nous souffrons d'un biais de sélection rétrospectif si nous pensons que la prédiction moyenne et l'observation moyenne devraient être les mêmes pour les éléments à évolution "lente", "moyenne" et "rapide". Nous devons vivre avec et accepter l'écart entre les deux colonnes. Heureusement, nous pouvons utiliser le théorème de Bayes pour obtenir la valeur attendue réaliste. Une solution consiste donc à ajouter au tableau une colonne contenant la valeur théoriquement attendue de la prédiction moyenne par godet, qui peut être comparée à la prédiction moyenne réelle dans ce godet. En d'autres termes, nous pouvons quantifier et reproduire théoriquement le biais de sélection rétrospectif et voir si les données agrégées correspondent aux attentes théoriques.
Une solution beaucoup plus simple consiste toutefois à poser des questions différentes aux données, à savoir des questions qui s'alignent sur ce que les prévisions nous promettent. Cela nous permet de vérifier directement si ces promesses sont tenues ou non : Au lieu de regrouper les résultats par catégories, nous les regroupons par catégories de prédiction, c'est-à-dire en fonction des ventes prédites ( lentes, moyennes et rapides). Il s'agit ici de vérifier si la promesse de la prévision (la moyenne des ventes pour une certaine prévision correspond à cette prévision) est respectée. Pour notre exemple, nous obtenons ce tableau :
| Fréquence des ventes prévue | Moyenne des ventes observées | Prévision moyenne |
| Lenteur <3 pièces/jour | 1.288 | 1.267 |
| Moyen 3 pièces/jour | 5.247 | 5.229 |
| Rapide >3 pièces/jour | 12.855 | 12.950 |
En tenant compte du nombre total de mesures, un test de signification statistique serait négatif, c'est-à-dire qu'il ne montrerait pas de différence significative entre la moyenne des ventes observées et la moyenne des prévisions. Nous en concluons que notre prévision est non seulement globalement non biaisée, mais également non biaisée par strate de prédiction.
En général, vous pouvez évaluer une prévision en filtrant toutes les informations connues au moment de la prédiction, et la prévision doit être impartiale dans tous les tests. Toutefois, le filtre n'est pas autorisé à contenir des informations futures telles que les fluctuations aléatoires qui se produisent dans les observations, sur lesquelles la nature ne se prononce que dans le futur du point de prédiction dans le temps.
Que devez-vous retenir si vous êtes arrivé jusqu'ici ? (1) Lorsque vous sélectionnez par résultat, vous ne disposez pas d'un échantillon représentatif. (2) Soyez sceptique à l'égard de vos propres attentes - des attentes intuitives très raisonnables se révèlent erronées. (3) Rendez vos attentes explicites et testez-les par rapport à des cas bien compris.













