Dans le domaine de la prévision pour le commerce de détail, la quantité d'intérêt est la demande des clients pour un certain produit, par exemple le nombre de paniers de fraises demandés. Dans la pratique, on observe une quantité légèrement mais significativement différente, à savoir les ventes enregistrées. Les ventes reflètent la demande, mais sont limitées par la capacité, c'est-à-dire par le niveau des stocks : Lorsque 20 paniers sont demandés, mais que 12 sont disponibles, seuls 12 sont vendus, et les 8 clients qui souhaitaient également acheter n'ont pas été satisfaits. La distinction entre les ventes et la demande peut sembler couper les cheveux en quatre, mais cet article de blog vous montrera pourquoi le fait de confondre les ventes et la demande conduit à des formations biaisées et à des évaluations de modèles erronées. Vous apprendrez comment les stocks limités influencent les ventes et comment contourner les principaux pièges pour aborder en toute confiance les situations réelles qui impliquent des stocks limités.
Demande et ventes
Quelle est la prévision la plus précise que vous puissiez imaginer, une prévision de la demande toujours juste sur laquelle vous pouvez placer n'importe quel pari ? Dans de nombreuses situations, la réponse est la suivante : Prévoyez simplement "0" en permanence ! Si la prévision de la demande est égale à zéro, aucun article ne sera commandé, aucun article ne sera mis en rayon, aucun article ne sera vendu. La prédiction zéro s'avère exacte et correspond parfaitement aux ventes zéro observées. Cette prévision absolument exacte n'est évidemment pas celle qui rendra votre directeur heureux.
Cet exemple extrême montre qu'il faut faire attention à ce que l'on demande : L'objectif d'un détaillant n'est pas de produire des prévisions précises, mais d'exploiter une entreprise durable. Ce paradoxe met également en lumière un dilemme fondamental de la prévision de la demande : La prévision elle-même influence le niveau de stock qui est finalement fourni, ce qui compromet son évaluation. Vous pourriez dire que cette influence existe pour de bonnes raisons, c'est pour cela que les prévisions ont été faites ! Mais le niveau de stock fixe une limite supérieure au nombre d'articles pouvant être vendus, ce qui restreint artificiellement les valeurs de vente qui peuvent être observées. Il en résulte une divergence entre la demande hypothétique ("quelle quantité est demandée") et les ventes observées ("quelle quantité a été vendue"). Les ventes observées correspondent à la demande réelle ou aux stocks disponibles, selon ce qui est le moins élevé.
Dans ce billet, je vous convaincrai qu'il n'y a aucun moyen d'éviter un traitement probabiliste rigoureux du problème de la demande par rapport aux ventes. La distinction entre la demande et les ventes, le traitement méticuleux de ces quantités et de ce que nous prévoyons et observons exactement sont essentiels pour une formation et une évaluation correctes et réussies des modèles.
Pour rendre les choses plus concrètes (et plus savoureuses), prenons l'exemple d'un détaillant qui vend des paniers de fraises fraîches. Le nombre de paniers vendus, qui est un nombre entier, peut alors être considéré comme des "pièces". Malheureusement, ces produits d'épicerie ultra-frais sont gaspillés lorsqu'ils ne sont pas vendus dans la journée. Par conséquent, les commandes excessives, c'est-à-dire le fait d'avoir en stock plus que ce qui est demandé, sont coûteuses et doivent être évitées. D'autre part, imaginez que vous ayez envie de fraises, mais qu'elles soient déjà en rupture de stock lorsque vous les cherchez dans votre supermarché local : Vous devenez un client frustré, dont la volonté de payer n'a pas été prise en compte. Par conséquent, la sous-commande, c'est-à-dire le fait d'avoir moins de stock que ce qui est demandé, est également coûteuse, tant en termes de satisfaction du client que de perte de revenus et de bénéfices.
Un détaillant doit commander le nombre adéquat de paniers de fraises afin d'équilibrer soigneusement le gaspillage et les ventes perdues. Bien entendu, pour résoudre ce problème de commande, il est nécessaire de disposer d'une prévision précise de la demande, qui permette de savoir combien de paniers sont demandés, et non combien sont vendus (rappelez-vous la prophétie "0" auto-réalisatrice évoquée plus haut).
Combien allons-nous vendre ?
Approfondissons les prévisions de la demande et analysons leur signification. Une prévision de la demande nous indique combien d'articles seront demandés. Mais que signifie exactement "9,7 paniers seront demandés" ? Il est évident que l'on ne peut pas vendre un nombre fractionnaire de paniers de fraises, l'interprétation littérale est ridicule. Néanmoins, nous acceptons et comprenons intuitivement la prévision, et nous l'interprétons comme une affirmation sur le nombre moyen attendu de paniers vendus, c'est-à-dire le nombre de paniers que nous vendons en moyenne lorsque la même situation se répète plusieurs fois (et que les stocks sont toujours suffisants, ce que nous supposerons pour l'instant). Par conséquent, nos prévisions cachent implicitement une certaine distribution de probabilité, c'est-à-dire une certaine conception de la probabilité de vendre 1, 2, 3, ... paniers, puisqu'elles n'indiquent que la moyenne des ventes attendues. La nature de ces probabilités, ou la proximité des observations individuelles (c'est-à-dire les chiffres de vente réels) autour de cette moyenne de 9,7, n'est pas mentionnée.
Soulevons le tapis sous lequel la distribution de probabilité a été cachée pour voir à quoi elle devrait ressembler. Nous utiliserons le tableau ci-dessous pour illustrer notre exemple. A priori, les distributions de probabilités avec une valeur d'espérance de 9,7 peuvent prendre des formes très différentes : Pensez à une probabilité de 51,5% de trouver zéro et à une probabilité de 48,5% de trouver 20, comme le montre le panneau de gauche. Il en résulte une moyenne de 9,7 - même si l'on n'observe jamais de valeurs proches de 9,7, telles que 9 ou 10, mais seulement des valeurs extrêmes telles que 0 ou 20. La distribution de probabilité du panneau du milieu attribue une probabilité de 70% à 10 et une probabilité de 30% à 9 ; elle porte également la valeur d'espérance 9,7, mais la masse de probabilité est beaucoup plus concentrée sur des valeurs proches de la moyenne, qui devient ainsi une bonne estimation du nombre typique de ventes. L'ensemble des distributions ayant une moyenne de 9,7 est infiniment grand, et la plupart de ces distributions se comporteront mal (ou seront "pathologiques", comme les mathématiciens aiment à le dire). Heureusement, nous pouvons supposer des distributions de probabilité simples et bien gérées, telles que la distribution de Poisson dans le panneau de droite (lisez l'article du blog Forecasting few is different pour savoir pourquoi il s'agit d'un choix raisonnable).
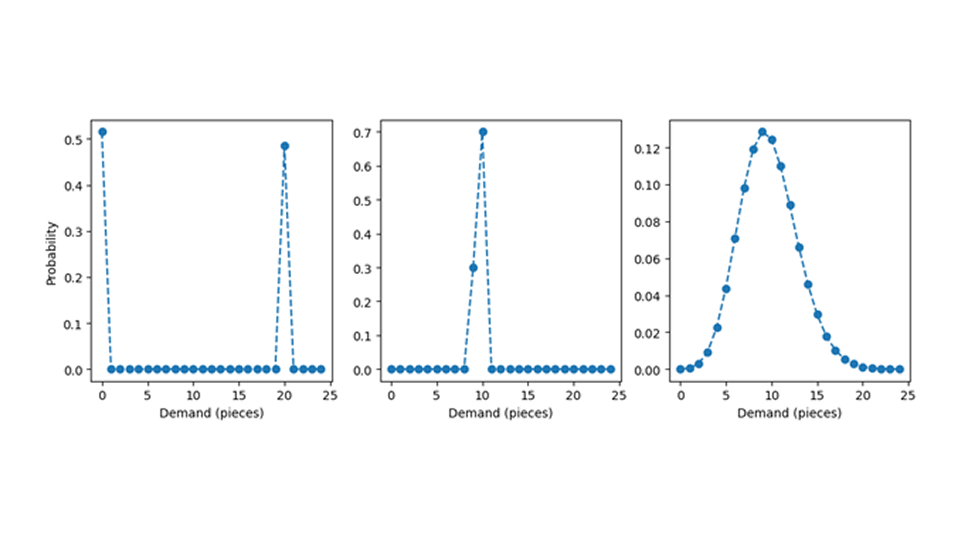
Tout au long de ce texte, nous supposons que la prévision produit la moyenne d'une distribution de Poisson prédite et que la demande est réellement distribuée selon une distribution de Poisson, c'est-à-dire que la prévision est correcte. Même ce scénario idéalisé comportera suffisamment de subtilités pour justifier un article de blog.
Comment les stocks finis censurent l'information
Accueillons maintenant la capacité finie dans le jeu. Étant donné une distribution de la demande, nous obtenons la distribution des ventes en faisant correspondre chaque valeur possible de la demande à la valeur des ventes qui en résulte. Pour toutes les valeurs de la demande qui sont inférieures ou égales au nombre de stocks disponibles, la demande se traduit simplement par des ventes dans une proportion de 1:1 : Lorsqu'il y a 12 paniers disponibles, 5 paniers demandés donnent lieu à 5 ventes, 12 paniers demandés donnent lieu à 12 ventes. Lorsque la demande est supérieure aux stocks, en d'autres termes, lorsque la capacité n'est pas suffisante, les ventes sont limitées par cette valeur de stock : Lorsque 13, 25 ou 463 paniers sont demandés, seuls 12 seront vendus. Lorsque l'ensemble des stocks est vendu, on parle de "capacity hit". La masse de probabilité associée à la demande de 13, 25 ou 463 paniers doit cependant "aller quelque part", et elle est effectivement ajoutée à la probabilité que les stocks totaux soient demandés. Les distributions des probabilités de vente pour une demande moyenne de 9,7 et différentes capacités (16, 12, 8) sont présentées dans la figure suivante.
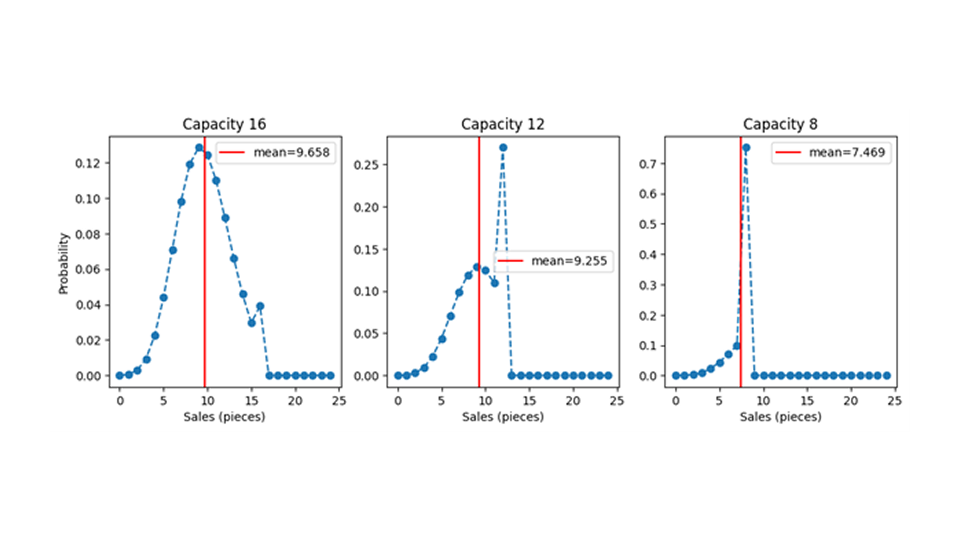
La capacité finie censure la demande d'une manière qui supprime l' information : Lorsque vous mettez en place une capacité de 16 et que vous observez un succès de capacité, c'est-à-dire 16 ventes, vous ne pouvez qu'en déduire que la demande était d'au moins 16 - et non de 16, 25 ou 7 624. La demande réelle a une valeur qui vous est inconnue - disons 47 - mais vous n'en observez que 16. En raison de la capacité limitée, nous perdons véritablement des informations de manière irrévocable (et pas seulement la satisfaction du client). Cette perte d'informations rend plus difficile l'apprentissage de modèles à capacité finie et leur évaluation.
Les graphiques montrent également les ventes moyennes attendues sous forme de lignes verticales rouges. Il est peut-être surprenant de constater qu'une capacité finie a un impact sur la valeur attendue des ventes, même lorsque la capacité reste supérieure à la demande attendue. En d'autres termes, lorsque vous prévoyez une demande de 9,7 et que vous fournissez 12 articles en stock, vous vendez moins de 9,7 en moyenne ! Vous devez stocker plus que prévu en moyenne pour vendre autant que prévu ! Cela peut prêter à confusion : Pour un événement donné, les ventes ne représentent que le minimum de la demande et des stocks. Mais la moyenne de la distribution de probabilité des ventes n'est pas nécessairement le minimum de la demande attendue et de la capacité, car la forme de la distribution de probabilité doit être prise en compte. La raison de ce comportement peut-être surprenant est que la valeur de la demande moyenne prévue repose sur des fluctuations autour de la moyenne qui s'annulent en moyenne. En d'autres termes, les fluctuations négatives (parfois, moins d'articles que 9,7 sont vendus) sont compensées par les fluctuations positives (parfois, plus d'articles que 9,7 sont vendus). Lorsque la capacité est finie, ces fluctuations positives nécessaires sont supprimées et l'annulation des fluctuations positives et négatives ne se produit plus. Cela pousse les ventes moyennes attendues vers des valeurs inférieures, même lorsque la capacité est supérieure à la demande moyenne attendue.
Le graphique suivant montre les ventes attendues en fonction de la capacité, toujours pour une demande attendue de 9,7. Lorsque la capacité est beaucoup plus importante que la demande prévue (environ 20), les événements affectés par la capacité finie sont rares. Par conséquent, le nombre attendu de ventes reste inchangé et proche de 9,7. Lorsque la capacité est faible, par exemple 5, il est presque inévitable que la capacité soit atteinte et, en moyenne, une valeur proche de cette capacité est vendue. Entre 7 et 14 ans environ, une transition s'opère, la capacité a un impact fort, mais pas totalement déterminant sur les ventes.
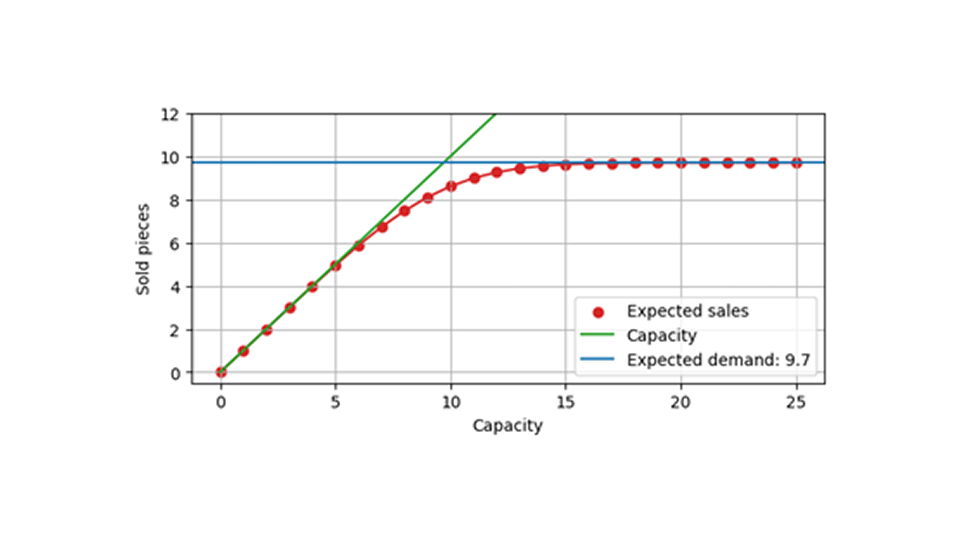
Formation et évaluation de modèles sur une demande censurée
Maintenant que nous maîtrisons notre cheval de bataille - la distribution de probabilité des ventes, alias la distribution de la demande censurée par la capacité - comprenons ce à quoi nous devons faire attention lorsque nous formons et évaluons des modèles dans de telles circonstances.
Il faut distinguer les différents régimes. Si la capacité était atteinte chaque jour, on ne connaîtrait jamais la véritable demande, mais seulement une limite inférieure ("nous avons vendu 5 pièces, la demande a donc été d'au moins 5"). Heureusement, ce scénario n'est pas réaliste : Lorsque la capacité est atteinte tous les jours, nous avons affaire à de nombreux clients mécontents et à de nombreuses demandes non satisfaites - aucun détaillant ne pourra maintenir un tel mode de fonctionnement pendant longtemps. S'ils y sont contraints par des restrictions de l'offre, ils peuvent envisager d'orienter la demande en augmentant les prix.
À l'autre extrême, lorsque la capacité n'est jamais atteinte, nous bénéficions d'un régime doux pour faire de la science des données : Nous lisons la demande réelle tous les jours, nous pouvons essentiellement négliger toutes les discussions sur la capacité. Mais le rêve du scientifique des données est le cauchemar du responsable du développement durable : une telle stratégie de commande entraînerait une énorme quantité de déchets. Compte tenu d'une demande attendue de 9,7, nous devrions conserver 21 articles en stock pour ne tomber en rupture de stock qu'une fois tous les 1 000 jours.
Par conséquent, on rencontre généralement une situation dans laquelle la demande atteint parfois la capacité (et le produit est épuisé à un moment donné de la journée), et parfois non (et il reste des stocks dans la soirée). Cela est raisonnable, car il est souhaitable de trouver un compromis entre les objectifs concurrents d'éviter les déchets et d'éviter les ruptures de stock.
Nous devons reconnaître que la construction du meilleur modèle possible est en contradiction avec la gestion de la meilleure entreprise possible : Dans le cadre d'une stratégie commerciale durable (où les déchets ne sont pas totalement "gratuits", mais sont évités au moins dans une certaine mesure), il est inévitable que des produits soient parfois en rupture de stock. Cependant, la meilleure science des données est celle qui est réalisée lorsque les ruptures de stock sont garanties et que chaque valeur de vente reflète directement la demande. Puisque nous faisons de la science des données dans un contexte commercial, nous devrons vivre avec le scénario intermédiaire et les ruptures de stock occasionnelles.













