Lorsqu'il s'agit de prévisions de ventes concernant des articles à rotation rapide ou lente, nous devons tenir compte de l'échelle non proportionnelle de l'incertitude relative des prévisions avec les taux de vente, qui détermine largement le niveau de précision réalisable.
- Pour une même qualité de prévision, les prévisions concernant les objets à faible déplacement sont inévitablement assorties d'une erreur absolue plus faible mais d'une erreur relative plus élevée que celles concernant les objets à déplacement rapide. Évitez le piège de l'échelle naïve : si votre prévision semble avoir des difficultés avec les vendeurs lents, évaluez dans quelle mesure l'augmentation de l'erreur relative lorsque l'on passe à des vitesses faibles est attendue.
- Il n'y a pas de frontière stricte entre les personnes qui se déplacent "lentement" et celles qui se déplacent "rapidement". Ne catégorisez pas les éléments selon différentes méthodes d'évaluation, mais assurez-vous que votre évaluation traite tous les taux de vente prévus de manière appropriée.
- Votre analyse comporte-t-elle de nombreux éléments très lents ? Remettez en question cette évaluation et assurez-vous que votre échelle de temps d'agrégation correspond à la réalité de l'entreprise - vous ne prenez pas de décisions commerciales quotidiennes sur des produits non périssables à faible rotation.
À l'étranger, goûtez aux spécialités locales, fraîches et périssables.
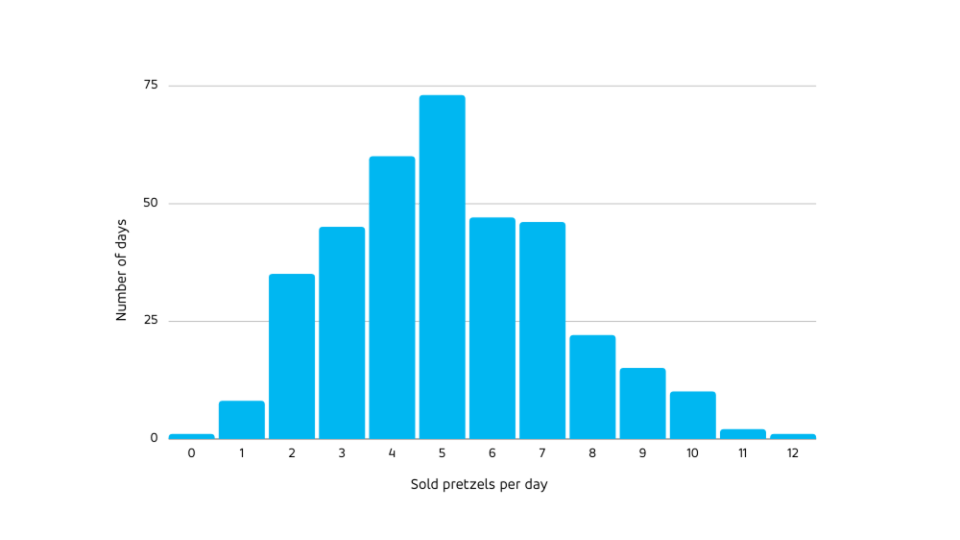
Les voyages, même s'ils ne sont pas faciles en période de pandémie, sont l'occasion de découvrir d'autres cultures, d'autres paysages et, bien sûr, de savourer de bons plats. Même dans le monde connecté et globalisé d'aujourd'hui, avec des détaillants multinationaux qui tentent de satisfaire instantanément tous les souhaits possibles partout sur la planète, certains produits ne sont tout simplement pas proposés du tout dans certains endroits. Vous ne vous attendez peut-être pas à recevoir ce conseil dans un article de blog sur le comptage des statistiques, mais c'est une conséquence directe de notre discussion ci-dessous : Pour tirer le meilleur parti de votre voyage à l'étranger sur le plan culinaire, explorez les spécialités fraîches ultra-périssables. Essayez les fruits frais à Rio de Janeiro, les bretzels chauffés au four à Munich et les fruits de mer crus à Busan.
En effet, il est difficile de trouver des bretzels bavarois traditionnels à Busan, il est impossible d'acheter des concombres de mer crus à Rio de Janeiro (pour autant que nous le sachions), et les voyageurs d'Amérique du Sud s'amusent du choix restreint de fruits frais dans les supermarchés d'Europe du Nord. Quels sont les aspects communs de ces produits ? Ils sont tous deux périssables et constitueraient un marché de niche s'ils étaient vendus en dehors de leur lieu d'origine . En effet, vous trouverez du kim chi mariné, de la bière Oktoberfest exportée et de la cachaça dans le monde entier. Mais les produits que les détaillants qualifieraient à la fois d'"ultrafrais" (très périssables, bons pour un jour ou deux) et de "vente lente" (susceptibles de ne pas se vendre un jour donné) ne sont jamais proposés, jamais, nulle part.
Comment cela se fait-il ? Pourquoi les supermarchés brésiliens n'essaient-ils pas de satisfaire la demande, certes minime, mais bel et bien existante, de concombre de mer cru ? Si 100 concombres de mer sont vendus chaque jour dans un magasin de Busan et que la demande est d'un concombre par jour à Rio de Janeiro, pourquoi les détaillants coréens répondent-ils à la première demande, alors que les magasins brésiliens ne répondent pas à la seconde ? Quelle est la différence fondamentale entre un produit périssable qui se vend rapidement - par exemple, une fraise en Europe - et un produit qui se vend lentement - par exemple, un concombre de mer cru au Brésil ?
Il s'avère que les détaillants ne proposent pas d'articles extrêmement peu demandés parce qu'ils ne peuvent pas prévoir la demande réelle avec suffisamment de précision pour trouver un point d'équilibre rentable entre les pertes et les ruptures de stock. En règle générale, l'activité d'un détaillant consiste à transformer la demande des consommateurs en ventes réelles. Pour savoir ce qu'il faut avoir en stock et en quelle quantité, ils doivent estimer la demande future le mieux possible, que ce soit par le biais de prévisions traditionnelles, basées sur l'intuition humaine, ou par le biais de statistiques modernes - ou même de prévisions basées sur l'apprentissage automatique. Jusqu'à il y a quelques années, les prévisions dans la chaîne d'approvisionnement concernaient de grandes quantités à des échelles grossières, par exemple les ventes totales de produits laitiers dans une région au cours d'un mois. Les chiffres typiques que l'on traite sont de l'ordre de quelques centaines au moins, jusqu'à plusieurs milliers. Les ressources informatiques actuelles permettent d'établir des prévisions à un niveau beaucoup plus granulaire, les prévisions se rapportant à des articles individuels pour un jour donné dans un lieu donné. À ce niveau, les chiffres typiques que nous traitons ne sont pas de l'ordre de 100 000, mais parfois de l'ordre de 5, 1 ou 0,1. Pouvons-nous simplement transférer les outils établis pour l'évaluation des prévisions du "monde des grands nombres" vers le "monde des petits nombres" ?
Techniquement, aucun problème ne se pose : Un programme informatique écrit pour les grands nombres peut être exécuté sur les petits nombres. D'un point de vue fonctionnel, cependant, nous devons être prudents : Lorsque l'on passe au régime des petits nombres, les idiosyncrasies statistiques, que l'on pouvait ignorer en toute sécurité dans le régime des ventes rapides, deviennent pertinentes, voire dominantes. Lorsque l'on s'oriente vers des vendeurs lents, on commence à percevoir les limites de la technologie de prévision : Comme toute technologie, la prévision a des limites fondamentales insurmontables. La précision de la prévision, c'est-à-dire l'écart de la demande réelle par rapport à la valeur prévue, et l'exactitude de la prévision, c'est-à-dire l'absence de biais en faveur de valeurs systématiquement grandes ou petites, ne peuvent pas toujours dépasser certaines valeurs, qui sont régies par des lois statistiques. Nous nous concentrons ici sur la limite inférieure de la précision des prévisions, sur le niveau inévitable de bruit dont souffre une prévision d'une quantité dénombrable. Cette limite s'avère dépendre de l'échelle: L'incertitude relative avec laquelle nous devons vivre est plus importante dans le cas des vendeurs lents que dans celui des vendeurs rapides. Cela implique à la fois que notre méthodologie d'évaluation des prévisions doit tenir compte de l'échelle et que l'on ne vous proposera pas de concombre de mer frais à Rio de Janeiro.












.png%3Fh%3D480%26iar%3D0%26w%3D640&w=1920&q=75)